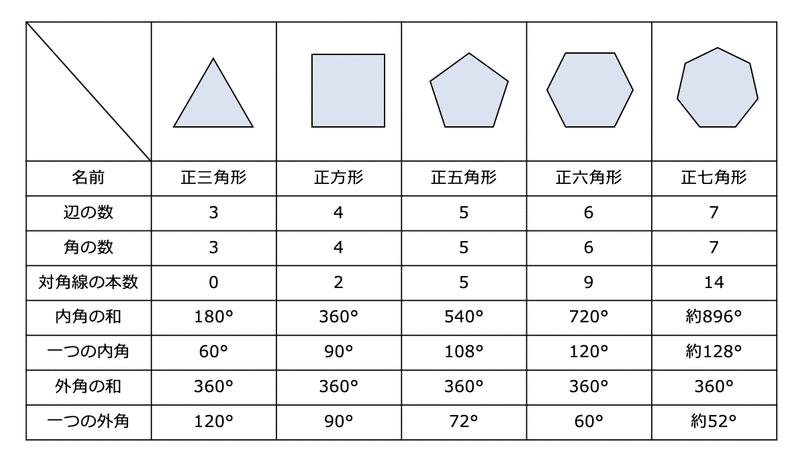
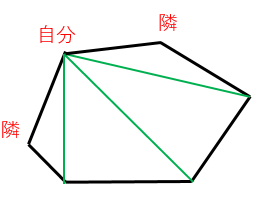
正n角形の対角線の数を求める公式を次の1から3の手順で導け。ただし、nは4以上の整数とする。 1正n角形のn個の頂点の中から2個を選ぶ選び方の総数を求める 2隣り合う2つの頂点を選ぶときの選び方の総数を求める 3①で求めた総数をひく 大至急お願いいたしますm(__)m十角形の場合,一つの頂点から引ける対角線の本数は 10-3=7(本). 自分自身と両隣には対角線を引けませんが,それ以外の7つの頂点には対角線を引ける. 頂点は全部で10個あるので,7x10=70(本). ただし,それだと同じ対角線を二度ずつ数えて内角の和は°、対角線の本数は5049本である。 正百二角形 正百二角形においては、中心角と外角は3529°で、内角は°となる。 一辺の長さが a の正百二角形の面積 S は = (/) を有理数と

多角形の対角線の作図は正確に書けると子供達は必ずはまります この喜びが子供を育ててくれます 七田式天六教室 本町教室及び魔法の折り紙オンライン教室は算数 数学のスペシャリストを育てます
正十二角形 対角線 交点
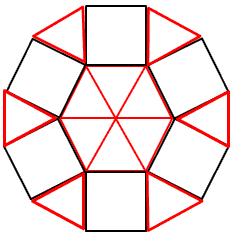
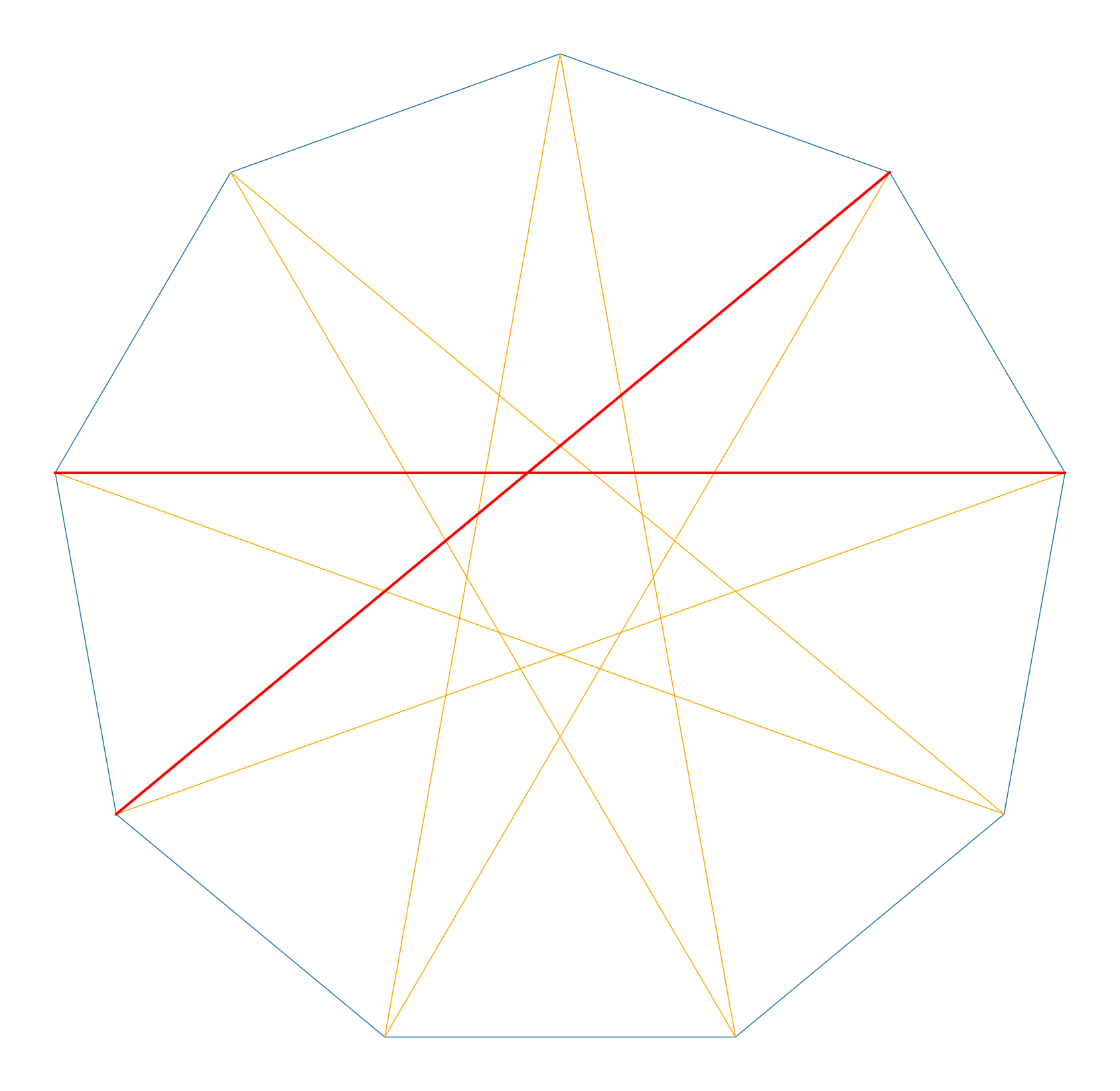
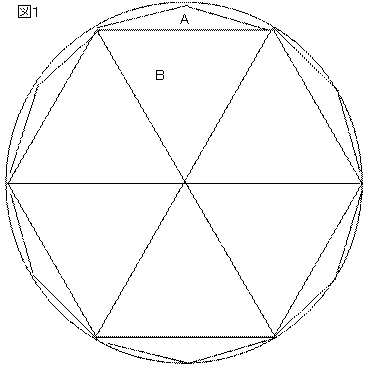
正十二角形 対角線 交点-右の図では、辺cdはもとの正八角形の頂点pの両どなりの頂点を結ぶ対角線ウの一部です。 このような対角線は全部で8本ありますから、ここでも正八角形が1つできて、 あわせて2つできるわけです。 正十二角形の場合は、どうでしょうか。 (3) 正十二角形のすべての頂点から対角線を引くと、 \(12\) 個の合同な二等辺三角形ができる。 この三角形の頂角は \(360^\circ \div 12 = 30^\circ\)
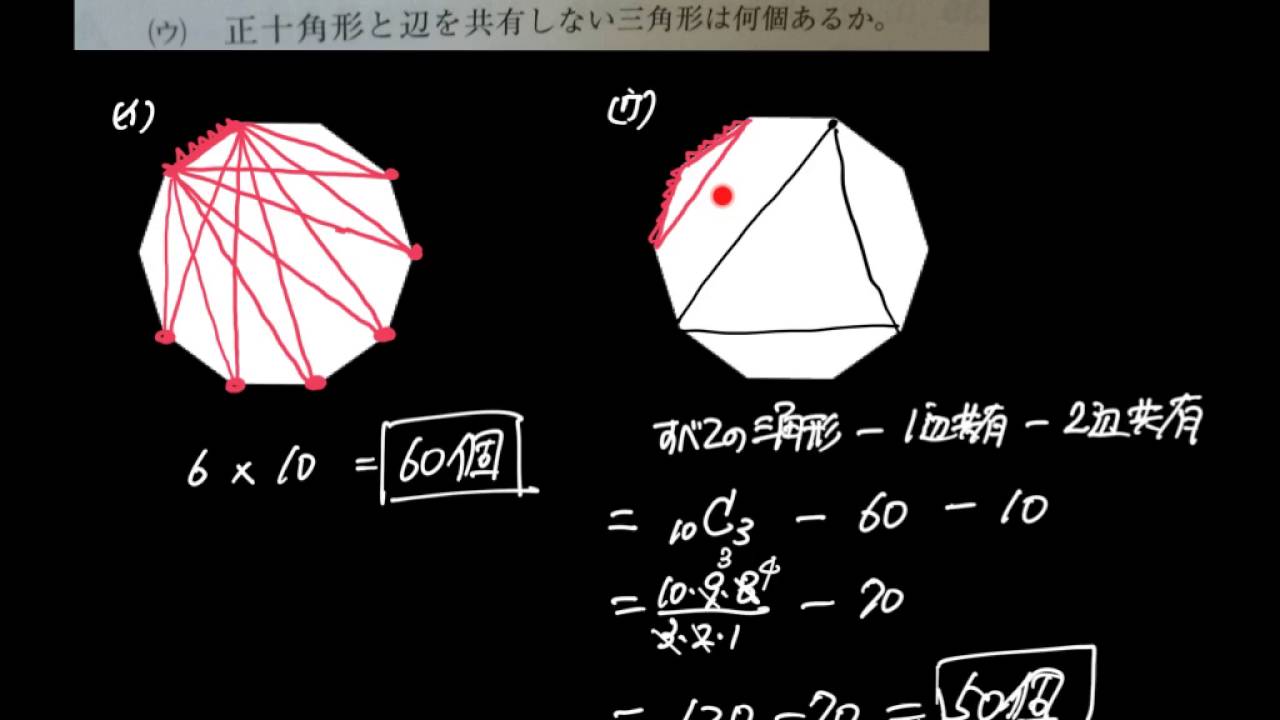



数a 正10角形 一辺を共有する三角形 Youtube
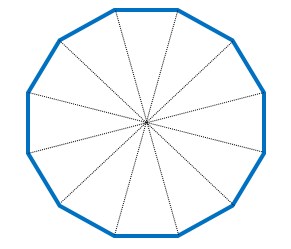
十二角形(じゅうにかくけい、じゅうにかっけい、dodecagon)は、多角形の一つで、12本の辺と12個の頂点を持つ図形である。 内角の和は1800°、対角線の本数は54本である。 正十二角形においては、中心角と外角は30°で、内角は150°となる。 一辺の長さが a の正十二角形の面積Sは(3)正十二面体は,立方体(一辺の長さは正五 角形の対角線)の各面に屋根図1を付けた 形である。 対角線の長さを とおくと,トレミ-の定理に より, から より, また,ABの中点をMとすると正十二角形の対角線の本数は何本ですか。 (解説) (問題) 七角形の対角線の本数は何本ですか。 (解答) (7-3)×7÷2=14 14本 四谷大塚 予習シリーズ のテキストは四谷大塚よりお買い求め下さい。 著作権は 中学受験の算数・理科ヘクトパスカル に
正多角形の場合の数 正多角形の対角線の数、正多角形の頂点で作る三角形についての場合の数を考えます。 正八角形ぐらいまでなら手書きで考えられるかもしれませんが、それ以上になると手書きでは難しいと思います。 一般化して正n角形で考えてみる十二角形 (じゅうにかくけい、じゅうにかっけい、 dodecagon )は、 多角形 の一つで、12本の 辺 と12個の 頂点 を持つ 図形 である。 内角 の 和 は1800°、 対角線 の本数は54本である。 正十二角形 対角線 正12角形の場合は 2本の対角線の交点が228個 3本の対角線の交点が60個 4本の対角線の交点が12� 十二角形 (じゅうにかくけい、じゅうにかっけい、 dodecagon )は、 多角形 の一つで、12本の 辺 と12個の 頂点 を持つ 図形 である。
E 7 i y l F ӂ ̂ 炢 j } ̂悤 ɐ \ p ` ̕ӂ̂Ƃ ɁA O p ` ܂ B i F ̐ O p ` P Q j正多角形の重心は最長の対角線どうしの交点(正 2n 角形に限る)や外接円および内接円の中心に一致する。 正多角形は、角(辺)の数が増えるごとに 円 に近づいていくので、「周の長さ÷ 外接円 の 直径 」を角の数が多い正多角形で 計算 すると、 円周率 図では隣り合っている赤と青のそれぞれが1組180 です 正十二角形に図のように対角線を引くと、12-2=10個の三角形に分かれます。 だから、正12角形の一つの内角は、180 ×10÷12=150 です。 空色二等辺三角形のとんがった方の角の大きさは、150 -2×6 投稿者 m




七角形 Wikiwand



正17角形と正18角形
正十二角形 定期的な十二角形は、同じ長さの辺と同じ大きさの内角を有する図です。これには、12次の反射対称と回転対称の12本の線があります。正十二角形はシュレーフリ記号{12}で表され、切り捨てられた 六角形t {6}または2回切り捨てられた三角形tt {3として構成できます。 (正十二角形の一番長い対角線の長さ) 長方形は互いに頂点だけで接し、重ならない 各長方形は、隣の長方形と、2頂点または3頂点で接している。 全体で円形っぽい形をしている まずは、正十二角形を並べるところから。正六角形の1つの内角の大きさを求めなさい。 式 答え 正八角形の対角線の数を求めなさい。 式 答え 1つの外角の大きさが°であるのは正何角形か。 式 答え 内角の和が °であるのは、正何角形か。 式 答え 内角の和が °であるのは、正何角形か。 式 答え



たのしい算数 正多角形はキレイだからこそ キッズライト 公式サイト 福岡 西都小学校前の学童保育 学習塾 四谷大塚net 東進こども英語塾



Www Kyoto Be Ne Jp Rakuhoku Hs Buildupload Pdffile0225 Pdf
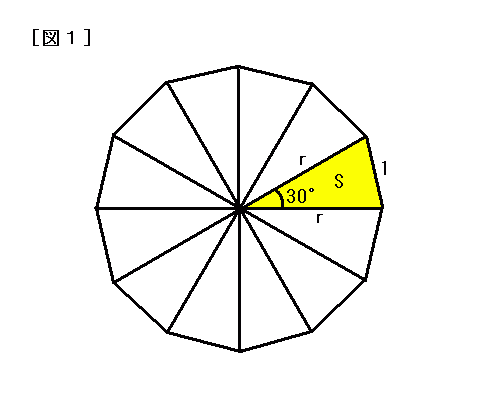
正十角形、正十二角形の一辺の長さを余弦定理を用いて求めた 正三角形 F 2 22 2 2 2 cos1 2 1 8 8 4 12 よってF 2 3 正方形 半径とG の長さの比は (半径):G = 2 :1より G 2 正方形の対角線凸n 角形(の辺および対角線)を m 角形(の辺あるいは対角線)で取りつくすという問題 定理1 凸n 角形の頂点を結んでできる線分,つまり辺または対角線はnC2 = 1 2 n(n¡1) 本である. 証明略 定理2 凸n 角形の頂点を結んでできる凸m 角形はnCm 個である. 証明略 例えば正n 角形などの場合,合同43正十二角形の折り方の模索 431正十二角形の性質 中心角と外角は30度,内角は150度である。対角線の本数は54本である。定規とコンパ 432正十二角形の折り方 正十二角形は折り紙で製作可能であることを明らかにし,その折り方を発見した。




高校数学 正十二角形の周長と面積 多角形の求積の原則 受験の月



多角形とは 外角 内角の和 面積 対角線の本数の公式と求め方 受験辞典
正12角形 対角線AI里怎么画圆角三角形,形状是我们画图时很容易用到的工具,它可以是多种多样的,今天来写一下圆角三角形的做法 三角形出现后,松开左键,画形状的时候同时按住shift键,就可以画出正三角形 4 ;正十二邊形是指所有邊等長、所有角等角的正奇数角形の場合は、 n C 4 (個) 正偶数角形の場合は、 n C 4 -Σk=3~?{(k C 2 -1)・a k} のような形で書けるのではないかと予想された。 凡人さんは、現在、次の問題点を研究中とのこと。 ・正奇数角形であれば、3本の対角線が1点で交わることが無いのか?正十二角形の分解 正十二角形の対角線を引いてできる三角形は、以前に記事に書いた 絶対に覚えるべきもうひとつの三角形。これを応用した問題は出やすいのではないかと思います。 また、一辺の長さが正十二角形の辺の長さと同じ正三角形と正方形で




正多角形の対角線の長さの種類 香料ゐっすゐの夢



コンパスで作図 正八角形の書き方がわかる5ステップ Qikeru 学びを楽しくわかりやすく
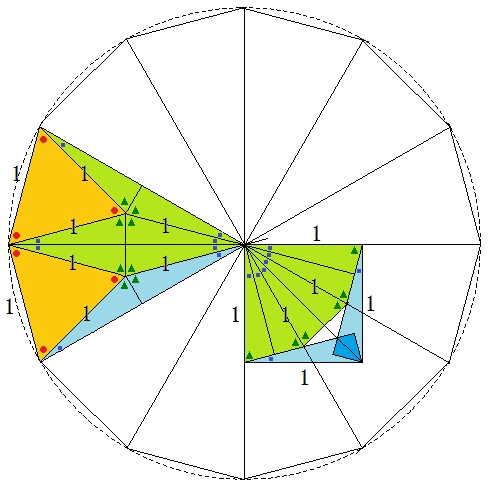
正十二角形の対角線の長さ・面積 正十二角形の 辺の長さを ,外接円の半径を ,内接円の半径を とする。 つの辺たとえば に対する弧 の中心角は ,円周角は , 正十二角形の内角は ,外角は である。思わず「お~~!!」と言いそうな良問を。受験算数の定番からマニアックな問題まで。図形ドリルでは,色々なタイプの図形問題を取り上げています。 図形ドリル 対角線の長さが2 cmの正方形6面と正六角形8面によって囲まれた立体について,体積は何cm3ですか。十二角形(じゅうにかくけい、じゅうにかっけい、dodecagon)は、多角形の一つで、12本の辺と12個の頂点を持つ図形である。 内角の和は1800 、対角線の本数は54本である。 正十二角形においては、中心角と外角は30 で、内角は150 となる�




十三角形 Wikipedia




おぉ 寒い寒い 正多角形の対角線
まず、正十二角形を対角線により十二等分します。 その内、「隣接した2つ分の面積」を考えましょう。 求める円の半径をrとすると、 (隣接した2つ分の面積)=r×r×1/2 となります。 (※「隣接した2つ分」に正三角形が隠れていますね) よって、十二角形(じゅうにかくけい、じゅうにかっけい、dodecagon)は、多角形の一つで、12本の辺と12個の頂点を持つ図形である。 内角の和は1800°、対角線の本数は54本である。 目次 1 正十二角形 11 正十二角形の作図;正十二角形 十二角形 (じゅうにかくけい、じゅうにかっけい、 dodecagon )は、 多角形 の一つで、12本の 辺 と12個の 頂点 を持つ 図形 である。 内角 の 和 は1800°、 対角線 の本数は54本である。



図形 正十二角形の分解 父ちゃんが教えたるっ



問題187 正十二角形の秘密
入試解説 6年生 男子校 5年生 正方形 正三角形 東京 兵庫 灘 算数オリンピック 共学校 面積比 円 図形NOTE logix出版 角度 1日目 直角三角形 4年生 女子校 相似 立方体 長方形 おうぎ形 30度 正六角形 16年 17年 19年 トライアル 18年 年 ファイナル 二等辺立方体 正十二面体 切稜率s さらにこのことから,2p角形面の対角線の長さの2乗は正十二角形 対角線 正12角形の場合は 2本の対角線の交点が228個 3本の対角線の交点が60個 4本の対角線の交点が12 十二角形 (じゅうにかくけい、じゅうにかっけい、 dodecagon )は、 多角形 の一つで、12本の 辺 と12個の 頂点 を持つ 図形 である 例題1 正五角形
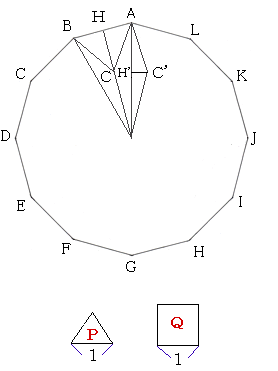



問題187 正十二角形の秘密




数a 正10角形 一辺を共有する三角形 Youtube
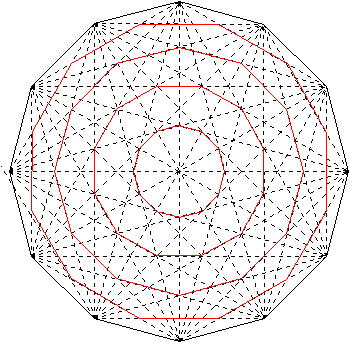
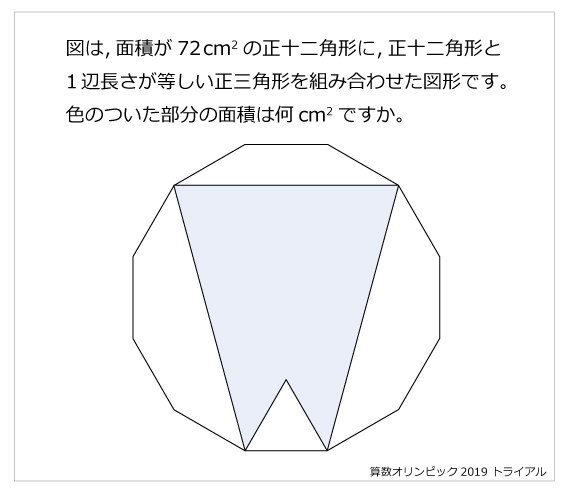
正十二角形の分解 正十二角形の 図は、面積が72㎝ 2 の正十二角形に、正十二角形と1 辺の長さが等しい正三角形を組み合わせた図形です。色のついた部分の面積は何㎝ 2 ですか。 解答 女子学院中 15年 正十二角形があります。ア~エはそれぞれ何度 正n角形の対角線の交点の数を求める式と その証明は https//arxivorg/PS_cache/math/pdf/9508/v3pdf 上によると正十二角形の対角線の交点の数は301個 正n角形の対角線の交点の数がnC₄ で求められるのはnが奇数のとき nが偶数のときは3本以上の対角線が1点で 交わることがあるので 交点の数を表わす式は 上記サイトのTheorem 1にあるような 複雑な式になる 式中でδm (n)はnがmの倍数のとき1 それ以外のとき0となる数として定義 正12角形の場合は 2本の対角線の交点が228個 3本の対角線出典 フリー百科事典『ウィキペディア(Wikipedia)』 十二角形 (じゅうにかくけい、じゅうにかっけい、 dodecagon )は、 多角形 の一つで、12本の 辺 と12個の 頂点 を持つ 図形 である。 内角 の 和 は1800°、 対角線 の本数は54本である。



入試問題編 作図 前田昌宏の中学受験が楽しくなる算数塾



1
正五角形に学ぶ (1)動機 五角形の性質をよく知りたいと思ったから (2)研究内容 1、正五角形の対角線が互いに分ける比(黄金比) 正五角形の1辺の長さをa、対角線をxとすると DFC∽ ACDより a x (x a) a よってx(x a) a2 x ax a2 0 2 a a 4 1 (a2) x 正十二角形の分解 正十二角形の対角線を引いてできる三角形は、以前に記事に書いた 絶対に覚えるべきもうひとつの三角形。 これを応用した問題は出やすいのではないかと思います。等高線 ご使用のブラウザは、JAVASCRIPTの設定がOFFになっているため一部の機能が制限されてます対角線の交点に関する正18 角形の性質を裏付けるために,対角線の交点の個数を調べてみた。 正n 角形の対角線の交点は,延べ ( 1)( 2)( 3) 24 1 n C4 = n n− n− n− 本 ある。これは,2 本の対角線の両端の4 点を与えれば交点が定まることによる。このうち,実際




正多角形の対角線



その1 驚き 正n角形の1頂点から他の頂点までの全線分の積はn
正十二角形の分解 正十二角形の対角線を引いてできる三角形は、以前に記事に書いた 絶対に覚えるべきもうひとつの三角形。 これを応用した問題は出やすいのではないかと思います。



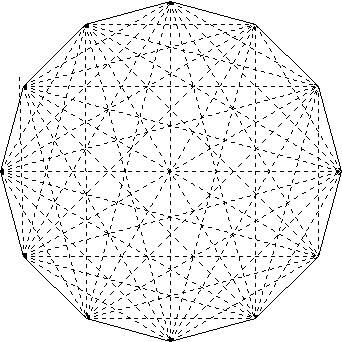
正多角形の対角線



対角線を描く すぐる学習会



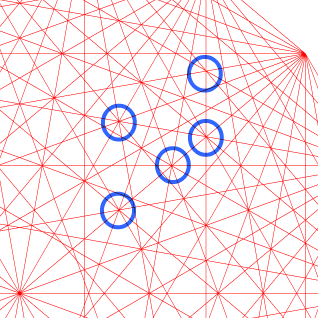
いろいろな正多角形をかいてみよう 家庭学習レシピ




正多角形 Wikipedia



入試問題に挑戦第4回




小5 算数 小5 54 正多角形 Youtube




Inkscape パソコン備忘録



問題187 正十二角形の秘密




十六角形 Wikipedia




素数誕生のメカニズム Art32pazuru なぜそんな形になってしまうんですか 正五角形にはペンタゴンーデカゴン定理や正多角形の角数nについて倍角数定理が存在しています 正多角形作図自由自在 正多角形第2定理 正多角形対角線定理 発想力教育研究所 素数誕生の



十角形 Wikipedia



正多角形の辺と対角線




正多角形の対角線 あなたと夜と数学と



多角形の対角線の本数を求める公式 具体例で学ぶ数学
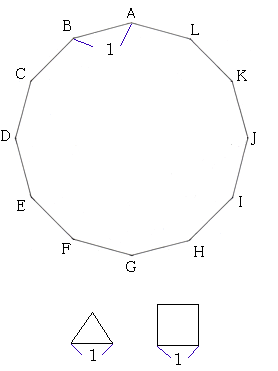



問題187 正十二角形の秘密



数学の図形問題です 正十二角形の対角線は何本引けますか 式もわかれば教えてく Yahoo 知恵袋




十二角形 Wikipedia



問題187 正十二角形の秘密



1




正多角形の対角線 あなたと夜と数学と



実践例 プログラミングで正多角形を学ぶ 山崎智仁 Tomohito Yamazaki Note
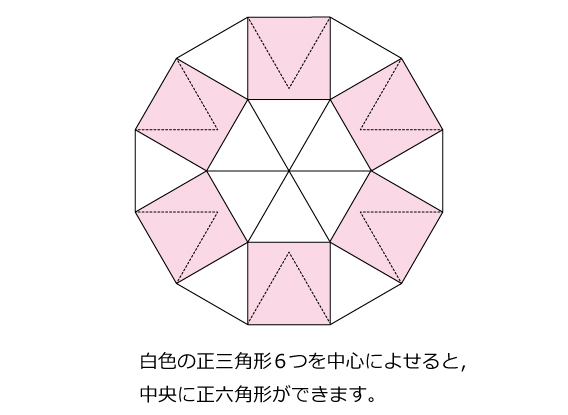



図形ドリル 第問 正十ニ角形と正三角形 算数星人のweb問題集 中学受験算数の問題に挑戦
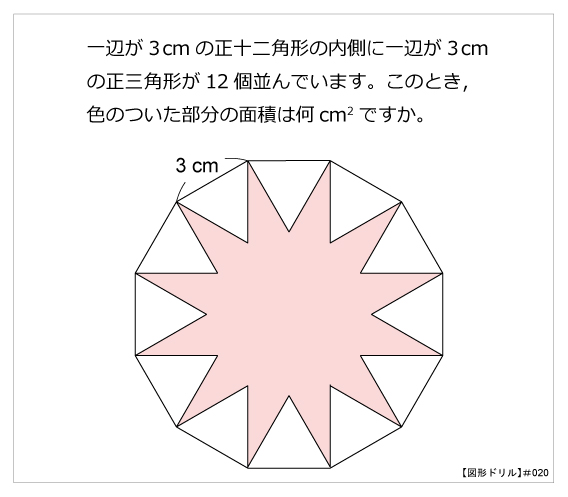



図形ドリル 第問 正十ニ角形と正三角形 算数星人のweb問題集 中学受験算数の問題に挑戦




正多角形の対角線
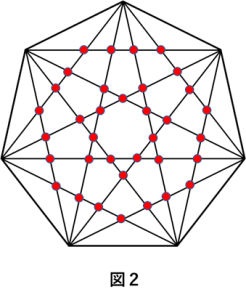



正九角形の対角線の交点の数を求める 中学受験プロ講師ブログ



正多角形とその対角線によって作られる正多角形の相似比 Yhoka Com



正多角形描画ソフト ソフトウェア 学校教育情報処理研究会




Trichoides على تويتر 正12角形の対角線は 54本あるらしい 切り絵



入試問題編 作図 前田昌宏の中学受験が楽しくなる算数塾




Inkscape 正多角形対角線を引いてみた パソコン備忘録



十一角形 Wikipedia



お久しぶりです 中学受験算数角度正多角形で対角線をひくと 角度は Yahoo 知恵袋



図形 正十二角形の分解 父ちゃんが教えたるっ




ポテト一郎 正七角形 正七角形の美しい性質を見つけました 赤の面積は青の面積の2倍になっています



正多角形の内接円の半径 倭算数理研究所



円周率3的世界 Part2



正多角形と方程式 X N 1 0 の不思議な関係 勉強法のバイブル 帝都大学へのビジョン




多角形の対角線の作図は正確に書けると子供達は必ずはまります この喜びが子供を育ててくれます 七田式天六教室 本町教室及び魔法の折り紙オンライン教室は算数 数学のスペシャリストを育てます



正12角形と対角線 麻布中学 2010年 イメージでわかる中学受験算数問題




高校数a 組合せ 多角形の頂点を結んで三角形を作る オンライン無料塾 ターンナップ Youtube




算数 53 正十二角形の面積 城北 平面図形 Youtube



正十二角形 算数星人のweb問題集 中学受験算数の問題に挑戦




面白い数学の問題 算数オリンピックからの挑戦 正十二角形の謎を解く そらの暇つぶしch



1




二十角形 Wikipedia
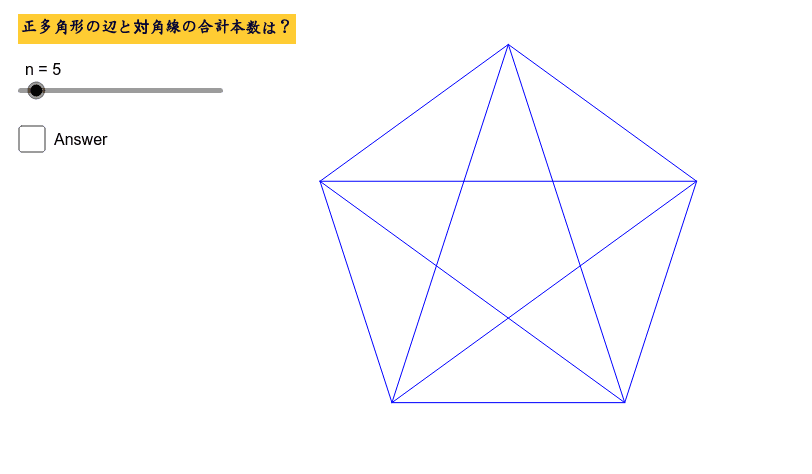



正多角形の辺 対角線の本数 Geogebra



図形 正十二角形の分解 父ちゃんが教えたるっ
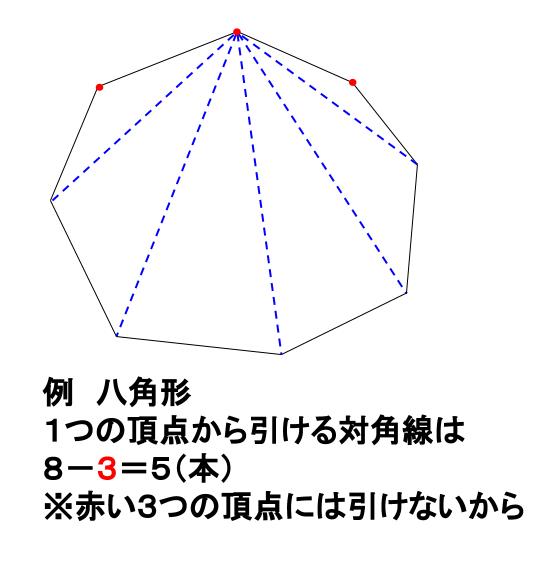



中学数学 多角形の対角線の本数 中学数学の無料オンライン学習サイトchu Su




対角線とは 多角形の対角線の本数の2通りの求め方 算数パラダイス



図形 正十二角形の分解 父ちゃんが教えたるっ



問題187 正十二角形の秘密




数a 場合の数 8角形 一辺を共有する三角形 Youtube



対角線 何本かな Gnolink 個別指導 グノリンク 知の力を活かせる人に




答1474 正十二角形の対角線でできる三角形の面積 ヤドカリの 気ままな数学



正多角形の対角線



正十二角形の対角線数は何本 奈良学園登美ヶ丘中学 12年 パズル算数クイズ




正多角形の中心線と垂直に交わる対角線による分割された線分の2乗の和 円周率近似値の日に生まれて理系じゃないわけないだろ Knifeのblog




中2の数学の図形の問題です 答えは 形 正十二角形 対角線の数 54本です Clear



問題187 正十二角形の秘密



1




おもしろ算数問題 シンプルで 複雑な計算も不要な正十二角形の問題 Youtube



Www Kyoto Be Ne Jp Rakuhoku Hs Buildupload Pdffile0225 Pdf




対角線とは 多角形の対角線の本数の2通りの求め方 算数パラダイス



多角形の対角線の本数を求める公式 具体例で学ぶ数学



小学5年の問題です もっとも長い対角線の長さが24 の正十二角形の面積を求め Yahoo 知恵袋




簡単公式 多角形の対角線の本数が5秒でわかる求め方 Qikeru 学びを楽しくわかりやすく



図形 正十二角形の分解 父ちゃんが教えたるっ




Uzivatel 大前誰今夏一 衒学ゴールデン Na Twitteru Dodecagon正十二角形と正方形の裁ち合わせ誰だっけpickover様だっけ 似たような話 でネタにしたいけど見当たらないspecial Thanks ある正多角形の対角線を一辺とする面積が同じ別の正多角形になる例が欲しいぞ




ハは肺魚のハ 跡地 直径10cmの正十二角柱型プリンの体積の求め方




頭の体操的問題 正十二角形の図形問題 仙台市立中等教育学校 年 自宅でできる受験対策ショップ ワカルー Wakaru




おもしろ算数問題 シンプルで 複雑な計算も不要な正十二角形の問題 Youtube




正二十四角形の対角線を幼稚園年長児に作図してもらっています みんな感動します 七田式天六教室 本町教室及び魔法の折り紙オンライン教室は算数 数学のスペシャリストを育てます




高校数学a 正多角形内の三角形の個数 二等辺三角形 正三角形 直角三角形 鈍角三角形 鋭角三角形他 受験の月




正多角形の対角線 あなたと夜と数学と




正多角形の対角線の長さ 香料ゐっすゐの夢



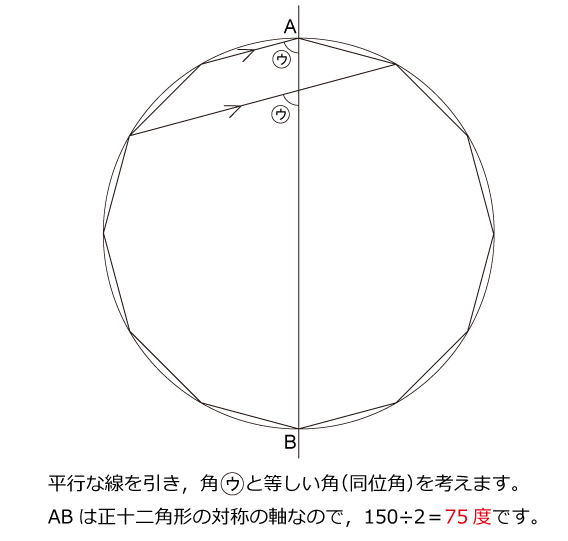
問題187 正十二角形の秘密



第390問の解答




Trichoides على تويتر 正12角形の対角線は 54本あるらしい 切り絵




正多角形の対角線



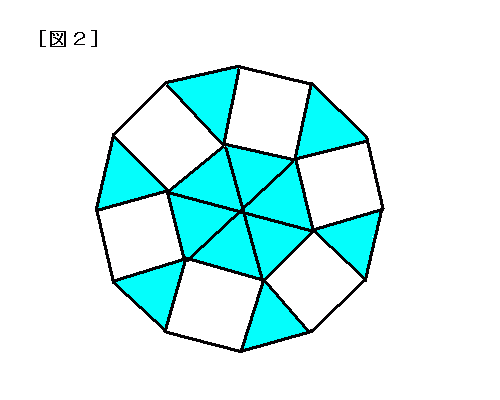
今年の1問 15年女子学院中 正十二角形 算数星人のweb問題集 中学受験算数の問題に挑戦
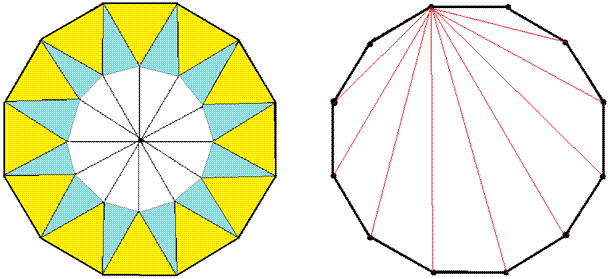



問題187 正十二角形の秘密




ベリースライム 正十二角形の性質 正十二角形の面積を3とすると 対角線を一辺とする正方形の面積は次のように表されます 算数 図形
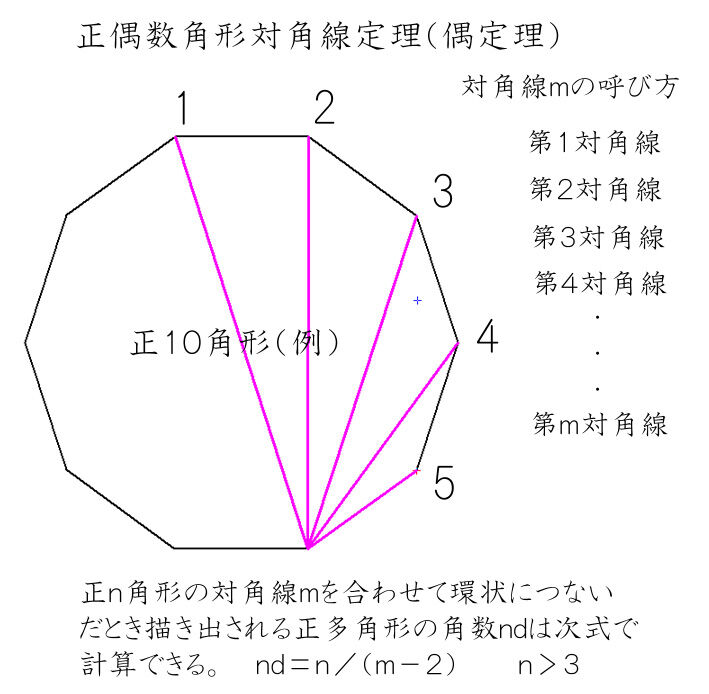



正多角形作図自由自在 正多角形第2定理 正多角形対角線定理 発想力教育研究所 素数誕生のメカニズム



図形 正十二角形の分解 父ちゃんが教えたるっ
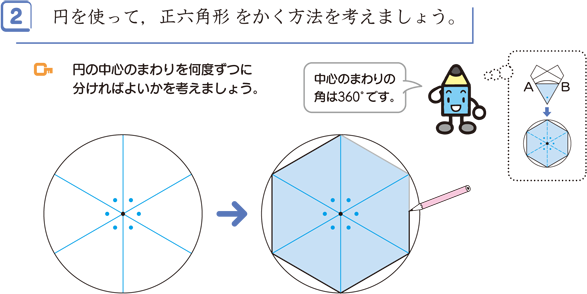



正多角形 算数用語集




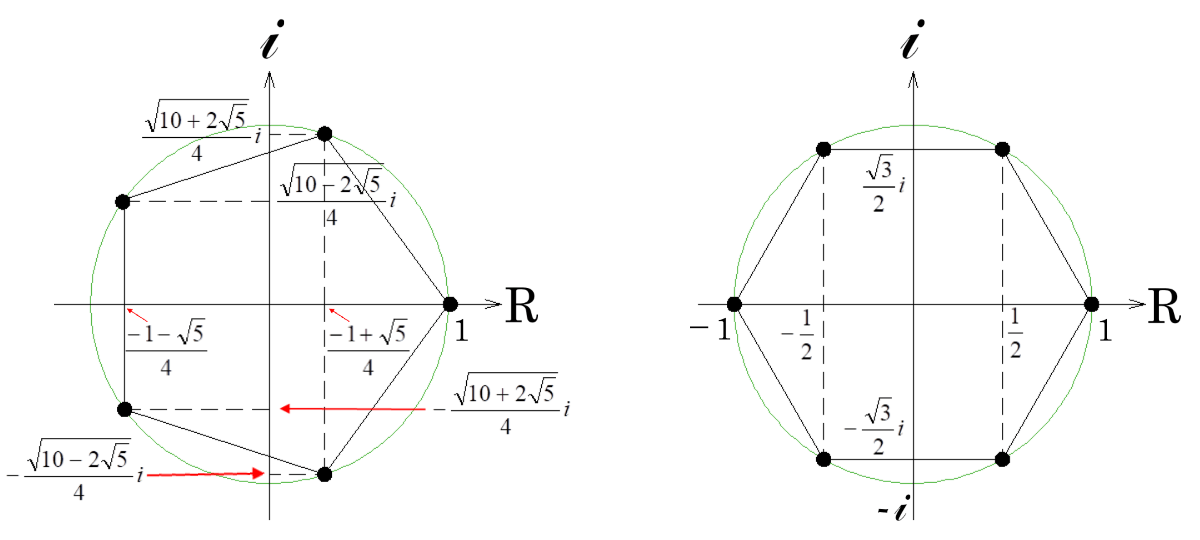
単位円に内接する正n角形の1つの頂点から他の頂点にひいた線分の積 数学の偏差値を上げて合格を目指す



0 件のコメント:
コメントを投稿